Daftar grup simetri bola hingga
 Simetri involusi Cs, (*) [ ] = |
 Simetri siklik Cnv, (*nn) [n] = |
 Simetri dihedral Dnh, (*n22) [n,2] = | |
| Grup polihedral, [n,3], (*n32) | |||
|---|---|---|---|
 Simetri tetrahedral Td, (*332) [3,3] = |
 Simetri oktahedral Oh, (*432) [4,3] = |
 Simetri ikosahedral Ih, (*532) [5,3] = | |
Grup simetri bola hingga juga disebut grup titik dalam tiga dimensi. Ada lima kelas simetri dasar yang memiliki domain dasar segitiga: dihedral, siklik, tetrahedral, oktahedral, dan simetri ikosahedral.
Artikel ini mencantumkan grup menurut notasi Schoenflies, notasi Coxeter,[1] notasi orbifold,[2] dan urutan. John Conway menggunakan variasi dari notasi Schoenflies, berdasarkan struktur aljabar grup kuaternion, diberikan label oleh satu atau dua huruf besar, dan subskrip bilangan bulat. Urutan grup didefinisikan sebagai subskrip, kecuali urutannya digandakan untuk simbol dengan plus atau minus, "±", awalan yang menyiratkan inversi pusat.[3]
Notasi Hermann–Mauguin (notasi internasional) juga diberikan. Grup kristalografi, total 32, adalah himpunan bagian dengan urutan elemen 2, 3, 4 dan 6.[4]
Simetri involusional
[sunting | sunting sumber]Ada empat grup involusial: tidak ada simetri (C1), simetri refleksi (Cs), Simetri rotasi lipatan 2 (C2), dan simetri titik pusat (Ci).
| Intl | Geo [5] |
Orb. | Schön. | Con. | Cox. | Uru. | Dom. Fundamental |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 11 | C1 | C1 | ][ [ ]+ |
1 | 
|
| 2 | 2 | 22 | D1 = C2 |
D2 = C2 |
[2]+ | 2 | 
|
| 1 | 22 | × | Ci = S2 |
CC2 | [2+,2+] | 2 | 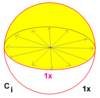
|
| 2 = m |
1 | * | Cs = C1v = C1h |
±C1 = CD2 |
[ ] | 2 | 
|
Simetri siklik
[sunting | sunting sumber]Ada empat famili simetri siklik tak hingga, dengan n = 2 atau lebih tinggi. (n mungkin 1 sebagai kasus khusus sebagai tidak simetri)
| Intl | Geo |
Orb. | Schön. | Con. | Cox. | Uru. | Dom. fundamental |
|---|---|---|---|---|---|---|---|
| 4 | 42 | 2× | S4 | CC4 | [2+,4+] | 4 | 
|
| 2/m | 22 | 2* | C2h = D1d |
±C2 = ±D2 |
[2,2+] [2+,2] |
4 | 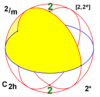
|
| Intl | Geo |
Orb. | Schön. | Con. | Cox. | Ord. | Dom. fundamental |
|---|---|---|---|---|---|---|---|
| 2 3 4 5 6 n |
2 3 4 5 6 n |
22 33 44 55 66 nn |
C2 C3 C4 C5 C6 Cn |
C2 C3 C4 C5 C6 Cn |
[2]+ [3]+ [4]+ [5]+ [6]+ [n]+ |
2 3 4 5 6 n |

|
| 2mm 3m 4mm 5m 6mm nm (n adalah nilai ganjil) nmm (n adalah nilai ganda) |
2 3 4 5 6 n |
*22 *33 *44 *55 *66 *nn |
C2v C3v C4v C5v C6v Cnv |
CD4 CD6 CD8 CD10 CD12 CD2n |
[2] [3] [4] [5] [6] [n] |
4 6 8 10 12 2n |

|
| 3 8 5 12 - |
62 82 10.2 12.2 2n.2 |
3× 4× 5× 6× n× |
S6 S8 S10 S12 S2n |
±C3 CC8 ±C5 CC12 CC2n / ±Cn |
[2+,6+] [2+,8+] [2+,10+] [2+,12+] [2+,2n+] |
6 8 10 12 2n |

|
| 3/m=6 4/m 5/m=10 6/m n/m |
32 42 52 62 n2 |
3* 4* 5* 6* n* |
C3h C4h C5h C6h Cnh |
CC6 ±C4 CC10 ±C6 ±Cn / CC2n |
[2,3+] [2,4+] [2,5+] [2,6+] [2,n+] |
6 8 10 12 2n |

|
Simetri dihedral
[sunting | sunting sumber]Ada tiga famili simetri dihedral tak hingga, dengan n = 2 atau tinggi (n mungkin 1 sebagai kasus khusus).
| Intl | Geo |
Orb. | Schön. | Con. | Cox. | Uru. | Dom. fundamental |
|---|---|---|---|---|---|---|---|
| 222 | 2.2 | 222 | D2 | D4 | [2,2]+ | 4 | 
|
| 42m | 42 | 2*2 | D2d | DD8 | [2+,4] | 8 | 
|
| mmm | 22 | *222 | D2h | ±D4 | [2,2] | 8 | 
|
| Intl | Geo |
Orb. | Schön. | Con. | Cox. | Uru. | Dom. fundamental |
|---|---|---|---|---|---|---|---|
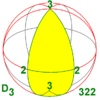
| 32 422 52 622 |
3.2 4.2 5.2 6.2 n.2 |
223 224 225 226 22n |
D3 D4 D5 D6 Dn |
D6 D8 D10 D12 D2n |
[2,3]+ [2,4]+ [2,5]+ [2,6]+ [2,n]+ |
6 8 10 12 2n |
|
| 3m 82m 5m 12.2m |
62 82 10.2 12.2 n2 |
2*3 2*4 2*5 2*6 2*n |
D3d D4d D5d D6d Dnd |
±D6 DD16 ±D10 DD24 DD4n / ±D2n |
[2+,6] [2+,8] [2+,10] [2+,12] [2+,2n] |
12 16 20 24 4n |

|
| 6m2 4/mmm 10m2 6/mmm |
32 42 52 62 n2 |
*223 *224 *225 *226 *22n |
D3h D4h D5h D6h Dnh |
DD12 ±D8 DD20 ±D12 ±D2n / DD4n |
[2,3] [2,4] [2,5] [2,6] [2,n] |
12 16 20 24 4n |

|
Simetri polihedral
[sunting | sunting sumber]Ada tiga jenis simetri polihedral: simetri tetrahedral, simetri oktahedral, dan simetri ikosahedral, dinamai berdasarkan segitiga wajah polyhedra biasa dengan simetri ini.
| Intl | Geo |
Orb. | Schön. | Con. | Cox. | Uru. | Dom. fundamental |
|---|---|---|---|---|---|---|---|
| 23 | 3.3 | 332 | T | T | [3,3]+ = [4,3+]+ |
12 | 
|
| m3 | 43 | 3*2 | Th | ±T | [4,3+] | 24 | 
|
| 43m | 33 | *332 | Td | TO | [3,3] = [1+,4,3] |
24 | 
|
| Intl | Geo | Orb. | Schön. | Con. | Cox. | Uru. | Dom. fundamental |
|---|---|---|---|---|---|---|---|
| 432 | 4.3 | 432 | O | O | [4,3]+ = [[3,3]]+ |
24 | 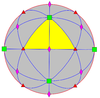
|
| m3m | 43 | *432 | Oh | ±O | [4,3] = [[3,3]] |
48 | 
|
| Intl | Geo | Orb. | Schön. | Con. | Cox. | Uru. | Dom. fundamental |
|---|---|---|---|---|---|---|---|
| 532 | 5.3 | 532 | I | I | [5,3]+ | 60 | 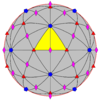
|
| 532/m | 53 | *532 | Ih | ±I | [5,3] | 120 | 
|
Lihat pula
[sunting | sunting sumber]Catatan
[sunting | sunting sumber]Referensi
[sunting | sunting sumber]- Peter R. Cromwell, Polyhedra (1997), Appendix I
- Sands, Donald E. (1993). "Crystal Systems and Geometry". Introduction to Crystallography. Mineola, New York: Dover Publications, Inc. hlm. 165. ISBN 0-486-67839-3.
- On Quaternions and Octonions, 2003, John Horton Conway and Derek A. Smith ISBN 978-1-56881-134-5
- The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [2]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380–407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559–591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3–45]
- N.W. Johnson: Geometries and Transformations, (2018) ISBN 978-1-107-10340-5 Chapter 11: Finite symmetry groups, Table 11.4 Finite Groups of Isometries in 3-space
Pranala luar
[sunting | sunting sumber]- Finite spherical symmetry groups
- (Inggris) Weisstein, Eric W. "Schoenflies symbol". MathWorld.
- (Inggris) Weisstein, Eric W. "Crystallographic point groups". MathWorld.
- Simplest Canonical Polyhedra of Each Symmetry Type, by David I. McCooey
