Penampang lintang radar
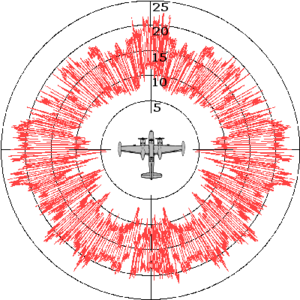
Penampang lintang radar (bahasa Inggris: radar cross-section, disingkat RCS), dilambangkan dengan σ, juga disebut jejak radar, adalah ukuran seberapa mudahnya suatu objek terdeteksi oleh radar. RCS yang lebih besar menunjukkan bahwa suatu objek lebih mudah terdeteksi.[1]
Sebuah objek memantulkan sejumlah energi radar kembali ke sumbernya. Faktor-faktor yang memengaruhi hal ini meliputi:[1]
- bahan yang digunakan untuk membuat target;
- ukuran target relatif terhadap panjang gelombang sinyal radar yang menerangi;
- ukuran absolut dari target;
- sudut insiden (sudut di mana berkas radar mengenai bagian tertentu dari target, yang tergantung pada bentuk target dan orientasinya terhadap sumber radar);
- sudut pantulan (sudut di mana sinar yang dipantulkan meninggalkan bagian target yang terkena; ini tergantung pada sudut insiden);
- polarisasi radiasi yang dipancarkan dan diterima sehubungan dengan orientasi target.
Meskipun penting dalam mendeteksi target, kekuatan pemancar dan jarak bukanlah faktor yang mempengaruhi perhitungan RCS karena RCS adalah sifat dari reflektifitas target.
Penampang lintang radar digunakan untuk mendeteksi pesawat terbang dalam berbagai variasi jarak. Sebagai contoh, pesawat siluman (yang dirancang untuk memiliki kemampuan deteksi yang rendah) akan memiliki fitur desain yang memberikan RCS rendah (seperti cat penyerap, permukaan datar, permukaan yang secara khusus dimiringkan untuk memantulkan sinyal ke tempat lain selain ke arah sumber), berlawanan dengan pesawat penumpang yang memiliki RCS tinggi (logam polos, permukaan bulat yang secara efektif menjamin pemantulan sinyal kembali ke sumber, banyak tonjolan seperti mesin, antena, dan lain-lain). RCS merupakan bagian integral dari pengembangan teknologi siluman radar, khususnya dalam aplikasi yang melibatkan pesawat udara dan rudal balistik.[2] Data RCS untuk pesawat militer saat ini sebagian besar sangat rahasia.
Dalam beberapa kasus, sangat menarik untuk melihat area di tanah yang mencakup banyak objek. Dalam situasi seperti itu, akan sangat berguna untuk menggunakan kuantitas terkait yang disebut penampang lintang radar yang dinormalisasi (normalized radar cross-section, NRCS), juga dikenal sebagai koefisien hamburan diferensial atau koefisien hamburan balik radar, dilambangkan dengan σ0 atau σ0 ("sigma nol"), yang merupakan penampang lintang radar rata-rata dari sekumpulan objek per satuan luas:
dengan:
- σ adalah penampang lintang radar dari objek tertentu, dan
- A adalah area di tanah yang terkait dengan objek tersebut.[3]
Lihat pula
[sunting | sunting sumber]- Jejak inframerah
- Kekuatan target
- Pemodelan elektromagnetik
- Penampang lintang hamburan balik
- Survivabilitas
- System Planning Corporation
Referensi
[sunting | sunting sumber]- ^ a b "Radar Cross Section, Optical Theorem, Physical Optics Approx, Radiation by Line Sources" di YouTube
- ^ Knott, Eugene; Shaeffer, John; Tuley, Michael (1993). Radar Cross Section, 2nd ed. Artech House, Inc. hlm. 231. ISBN 978-0-89006-618-8.
- ^ Ulaby, Fawwaz (1986). Microwave Remote Sensing: Active and Passive, Volume 2. Artech House, Inc. hlm. 463. ISBN 978-0-89006-191-6.
Bacaan lebih lanjut
[sunting | sunting sumber]Bagian daftar pustaka atau bacaan lanjutan ini kemungkinan memuat saran yang berlebihan atau bertentangan dengan pedoman. Pastikan bahwa artikel hanya memerlukan jumlah yang secukupnya untuk saran bacaan yang berimbang, sesuai topik, tepercaya, dan cukup diketahui; hilangkan publikasi yang kurang relevan atau berlebihan dengan sudut pandang yang sama bila perlu. Pertimbangkan pula untuk menggunakan teks yang sesuai sebagai kutipan baris atau buat artikel kepustakaan sendiri. (Februari 2024) |
- Shaeffer, Tuley and Knott. Radar Cross Section. SciTech Publishing, 2004. ISBN 1-891121-25-1.
- Harrington, Roger F. Time-Harmonic Electromagnetic Fields. McGraw-Hill, Inc., 1961. ISBN 0-471-20806-X
- Balanis, Constantine A. Advanced Engineering Electromagnetics. Wiley, 1989. ISBN 0-471-62194-3.
- “A Hybrid Method Based on Reciprocity for the Computation of Diffraction by Trailing Edges”David R. Ingham, IEEE Trans. Antennas Propagat., 43 No. 11, November 1995, pp. 1173–82.
- “Revised Integration Methods in a Galerkin BoR Procedure” David R. Ingham, Applied Computational Electromagnetics Society (ACES ) Journal 10 No. 2, July, 1995, pp. 5–16.
- “A Hybrid Approach to Trailing Edges and Trailing Ends” David R. Ingham, proceedings of the ACES Symposium, 1993, Monterey.
- “Time-Domain Extrapolation to the Far Field Based on FDTD Calculations” Kane Yee, David Ingham and Kurt Shlager, IEEE Trans. Antennas Propagat., 39 No. 3, March 1991, pp. 410–413.
- “Numerical Calculation of Edge Diffraction, using Reciprocity” David Ingham, Proc. Int. Conf. Antennas Propagat., IV, May 1990, Dallas, pp. 1574–1577.
- “Time-Domain Extrapolation to the Far Field Based on FDTD Calculations”Kane Yee, David Ingham and Kurt Shlager, invited paper, Proc. URSI Conf., 1989, San José .
Pranala luar
[sunting | sunting sumber]- (Inggris) Radar Cross Section, Optical Theorem, Physical Optics Approx, Radiation by Line Sources for detailed lecture on introduction to the Radar Cross-Section (RCS)
- (Inggris) Hip-pocket formulas for high-frequency RCS backscatter; useful reference sheet (PDF)
- (Inggris) Method to measure radar cross section parameters of antennas
- (Inggris) Puma-EM A high performance, parallelized, open source Method of Moments / Multilevel Fast Multipole Method electromagnetics code
- (Inggris) Radar Cross Section Reduction Course A GA Tech course geared toward techniques used to reduce radar signature
- (Inggris) Radar Tutorial provides great visuals of RCS

