Teorema dasar kalkulus
| Kalkulus |
|---|
Teorema dasar kalkulus menjelaskan relasi antara dua operasi pusat kalkulus, yaitu pendiferensialan dan pengintegralan.
Bagian pertama dari teorema ini, kadang disebut sebagai teorema dasar kalkulus pertama, menunjukkan bahwa sebuah integral tak tentu[1] dapat dibalikkan menggunakan pendiferensialan.
Bagian kedua, kadang disebut sebagai teorema dasar kalkulus kedua, mengizinkan seseorang menghitung integral tertentu sebuah fungsi menggunakan salah satu dari banyak antiturunan. Bagian teorema ini memiliki aplikasi yang sangat penting, karena ia dengan signifikan mempermudah perhitungan integral tertentu.
Teorema dasar kalkulus kadang-kadang juga disebut sebagai Teorema dasar kalkulus Leibniz atau Teorema dasar kalkulus Torricelli-Barrow.
Sejarah
[sunting | sunting sumber]Penyataan yang pertama kali dipublikasikan dan bukti matematika dari versi terbatas teorema dasar ini diberikan oleh James Gregory (1638-1675).[2] Isaac Barrow (1630-1677) membuktikan versi umum bagian pertama teorema ini, sedangkan murid Barrow, Isaac Newton (1643-1727) menyelesaikan perkembangan dari teori matematika di sekitarnya. Gottfried Leibniz (1646–1716) menyistematisasi ilmu ini menjadi kalkulus untuk kuantitas infinitesimal.
Pengertian geometri
[sunting | sunting sumber]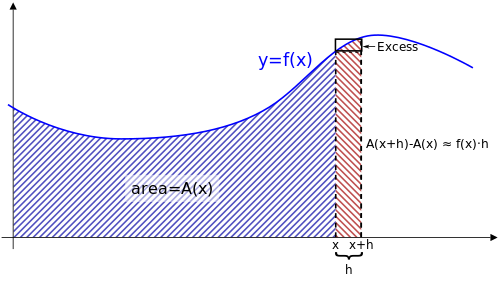
Untuk suatu fungsi kontinu yang grafiknya digambar sebagai kurva, setiap nilai memiliki fungsi luas berpadanan yang mewakilkan luas di bawah kurva antara dan . Fungsi tidak diketahui, tetapi mengingat bahwa fungsi tersebut mewakilkan luas di bawah kurva.
Luas di bawah kurva antara dan dapat dihitung dengan mencari luas di antara dan , lalu mengurangi luas di antara dan . Dengan kata lain, luas "strip" adalah .
Ada cara lain untuk mengestimasi luas strip tersebut. Seperti yang ditunjukkan dalam gambar di samping, dikali memperoleh luas persegi panjang yang kira-kira sama dengan luas strip. Jadi:
Nyatanya, estimasi ini mendekati kesamaan yang sempurna jika kita menambah bagian luas tambahan yang berwarna merah seperti di gambar. Jadi:
Dengan menyusun bentuk memperoleh:
- .
Ketika mendekati di limit, pecahan yang terakhir dapat ditunjukkan mendekati nol.[3] Ini benar karena luas daerah tambahan berwarna merah lebih kecil sama dengan luas dari batas persegi panjang hitam. Lebih tepatnya,
- ,
dengan dan adalah masing-masing titik ketika mendekati nilai maksimum dan minimum di selang . Melalui kekontinuan , bentuk terakhir mendekati nol sama seperti . Karena itu, ruas kiri mendekati nol sama seperti .
Ini menyiratkan . Artinya, turunan fungsi luas sama dengan fungsi asalnya, . Demikian juga, fungsi luasnya adalah antiturunan fungsi asalnya. Dengan menghitung turunan fungsi dan mencari luas di bawah kurvanya merupakan operasi "kebalikan". Pengertian ini merupakan bagian terpenting mengenai Teorema Dasar Kalkulus.
Intuisi
[sunting | sunting sumber]Secara intuitif, teorema ini dengan sederhana menyatakan bahwa jumlah perubahan infinitesimal suatu kuantitas terhadap waktu (atau terhadap kuantitas lainnya) akan menumpuk menjadi perubahan total kuantitas.
Untuk memahami pernyataan ini, diberikan sebuah contoh: Misalkan sebuah partikel berpindah mengikuti garis lurus dengan posisinya diberikan sebagai x(t), dengan t adalah waktu dan x(t) berarti x adalah fungsi dari t. Turunan dari fungsi ini sama dengan perbuahan infinitesimal kuantitas, dx, per perubahan infinitesimal waktu, dt (tentu saja turunannya sendiri tergantung pada waktu). Didefinisikan pula perubahan jarak terhadap perubahan waktu ini sebagai kecepatan v partikel. Dalam notasi Leibniz:
Dengan menata ulang persamaan ini, terlihat bahwa:
Dengan logika di atas, sebuah perubahan x (atau Δx) adalah jumlah dari perbuahan infinitesimal dx. Ia juga sama dengan jumlah dari hasil kali infinitesimal dari turunan dan waktu. Penjumlahahan takterhingga ini adalah pengintegralan; sehingga operasi penginteralan mengizinkan pemulihan fungsi semula dari turunannya. Dengan pemikiran yang sama, operasi ini juga dapat bekerja terbalik ketika kita menurunkan hasil dari sebuah integral untuk memulihkan turunan semula.
Pernyataan formal
[sunting | sunting sumber]Terdapat dua bagian teorema dasar kalkulus. Secara kasar, bagian pertama berkutat pada turunan sebuah antiturunan, sedangkan bagian kedua berkutat pada relasi antara antiturunan dan integral tertentu.
Bagian pertama
[sunting | sunting sumber]Bagian ini kadang-kadang dirujuk sebagai teorema dasar kalkulus pertama.
Misalkan f adalah fungsi bernilai real yang kontinu, didefinisikan pada sebuah interval tertutup [a, b]. Misalkan juga F adalah fungsi yang didefinisikan, untuk semua x pada [a, b], dengan
Maka F adalah kontinu pada [a, b], terdiferensialkan (differentiable) pada interval terbuka (a, b), dan
untuk semua x pada (a, b)
| Bukti untuk teorema dasar kalkulus bagian pertama |
|---|
|
Andaikan Misalkan terdapat dua bilangan x1 dan x1 + Δx pada [a, b]. Sehingga didapatkan dan Pengurangan kedua persamaan di atas menghasilkan Bisa ditunjukan bahwa
Dengan memanipulasi persamaan ini, kita dapatkan Substitusikan persamaan di atas ke (1), sehingga Menurut teorema nilai antara untuk pengintegralan, terdapat sebuah c pada [x1, x1 + Δx] sehingga Substitusikan persamaan di atas ke (2), kita dapatkan Bagi kedua sisi dengan Δx, menghasilkan
Dengan mengambil limit Δx → 0 pada kedua sisi persamaan: Ekspresi pada sisi kiri persamaan adalah definisi turunan dari F pada x1. Untuk mencari limit lainnya, kita gunakan teorema apit. c ada pada interval [x1, x1 + Δx], sehingga x1 ≤ c ≤ x1 + Δx. Juga, dan Sehingga menurut teori apit, Substitusikan ke (3), kita dapatkan Fungsi f kontinu pada c, sehingga limit dapat diambil di dalam fungsi. Oleh karena itu, kita dapatkan yang menyelesaikan pembuktian |
Bagian kedua
[sunting | sunting sumber]Bagian ini kadang-kadang dirujuk sebagai teorema dasar kalkulus kedua atau aksioma Newton–Leibniz.
Misalkan f adalah sebuah fungsi bernilai real yang kontinu, didefinisikan pada interval tertutup [a, b]. Misalkan juga F adalah antiturunan dari f, yakni salah satu dari fungsi-fungsi yang tak terhingga banyaknya yang untuk semua x pada [a, b],
Maka
| Bukti untuk teorema dasar kalkulus bagian kedua |
|---|
|
Ini adalah pembuktian limit menggunakan penjumlahan Riemann. Misalnya f kontinu pada interval [a, b], dan F adalah antiturunan dari f. Dimulai dengan kuantitas Misalkan pula terdapat bilangan-bilangan
sehingga Maka Sekarang kita tambahkan setiap F(xi) bersamaan dengan balikan aditif (inverse additive), sehingga kuantitas yang dihasilkan adalah sama: Kuantitas di atas dapat ditulis sebagai penjumalhan berikut: Kemudan kita akan menggunakan teorema nilai purata. Dinyatakan dengan singkat, Misalkan F kontinu pada interval tertutup [a, b] dan terdiferensialkan pada interval terbuka (a, b). Maka terdapat c pada (a, b) yang Sehingga Fungsi F terdiferensialkan pada interval [a, b]; sehingga ia juga terdiferensialkan dan kontinu pada setiap interval xi-1. Oleh karena itu, menurut teorema nilai purata, Substitusikan persamaan di atas ke (1), kita dapatkan Asumsi ini mengimplikasikan Juga, dapat diekspresikan sebagai dari partisi .  Perhatikan bahwa kita sedang menjelaskan luas persegi panjang, dengan lebar kali tinggi, dan kita menggabungkan total semua luas persegi panjang tersebut. Setiap persegi panjang, dengan teorema nilai purata, merupakan pendekatan dari bagian kurva yang digambar. Juga perhatikan bahwa tidak perlulah sama untuk setiap nilai , atau dengan kata lain lebar persegi panjang dapat berbeda-beda. Apa yang perlu kita lakukan adalah mendekatkan kurva tersebut dengan persegi panjang. Semakin kecil partisi ini dan semakin besar n, maka kita akan mendapatkan luas wilayah kurva yang semakin mendekati nilai sebenarnya. Dengan mengambil limit ekspresi norma partisi mendekati nol, kita mendapatkan integral Riemann. Yakni, kita mengambil limit partisi yang terbesar mendekati nol dalam hal ukuran, sehingga partisi-partisi lainnya lebih kecil dan jumlah partisi mendekati tak terhingga. Maka kita mengambil limit pada kedua sisi (2). Kita dapatkan Baik F(b) maupuan F(a) tidak bergantung pada ||Δ||, sehingga limit pada bagian sisi kiri tetaplah F(b) - F(a). Ekspresi pada sisi kanan persamaan merupakan definisi dari integral terhadap f dari a ke b. Sehingga kita dapatkan: yang menyelesaikan pembuktian. |
Korolari
[sunting | sunting sumber]Misalkan f adalah fungsi bernilai real yang didefinisikan pada sebuah interval tertutup [a, b]. Misalkan juga F adalah sebuah fungsi yang untuk semua x pada [a, b],
Maka untuk semua x pada [a, b],
dan
Contoh
[sunting | sunting sumber]Misalkan kita perlu menghitung
Di sini, dan kita dapat menggunakan sebagai antiturunan. Sehingga:
Atau lebih umumnya, misalkan kita perlu menghitung
Di sini, dan kita dapat menggunakan sebagai antiturunan. Sehingga:
Namun hasil ini akan lebih mudah didapatkan apabila menggunakan:
Perampatan
[sunting | sunting sumber]Kita tidak perlu mengasumsikan kekontinuan f pada keseluruhan interval. Bagian I dari teorema menyatakan: Jika f adalah setiap fungsi terintegral Lebesgue pada [a, b] dan x0 adalah bilangan pada [a, b] sehingga f kontinu pada x0, maka
terdiferensialkan untuk x = x0 dengan F'(x0) = f(x0). Kita dapat melonggarkan kondisi f lebih jauh dan andaikan bahwa ia hanyalah terintegralkan secara lokal/setempat. Pada kasus ini, kita dapat menyimpulkan bahwa fungsi F terdiferensialkan hampir di mana-mana dan F'(x) = f(x) hampir di mana-mana. Ini biasanya dikenal sebagai teorema pendiferensialan Lebesgue.
Bagian II dari teorema adalah benar untuk setiap fungsi terintegral (integrable fungction) Lebesgue f yang mempunyai sebuah antiturunan F (tidak semua fungsi terintegral mempunyainya).
Versi teorema Taylor yang mengekspresikan suku galat (error term) sebagai sebuah integral dapat dilihat sebagai sebuah perampatan (generalization) dari teorema dasar.
Terdapat sebuah versi teorema untuk fungsi kompleks: andaikan U adalah himpunan terbuka pada C dan f: U → C adalah fungsi yang mempunyai sebuah antiturunan holomorfik F pada U. Maka untuk setiap kurva γ: [a, b] → U, integral kurva dapat dihitung sebagai
Teorema dasar dapat dirampatkan ke integral kurva dan permukaan pada dimensi yang lebih tinggi dan pada manifold.
Salah satu pernyataan yang paling kuasa (powerful) adalah teorema Stokes: Diberikan M sebagai manifold mulus sesepenggal dimensi n berorientasi dan adalah sebuah bentuk n−1, yakni bentuk diferensial yang disangga secara kompak pada M kelas C1. Jika ∂M menandakan sempadan M dengan orientasi terinduksinya, maka
Di sini adalah turunan luar yang hanya terdefinisikan menggunakan struktur manifold.
Teorema ini sering kali digunakan dalam situasi ketika M adalah submanifold berorientasi terbenam (embedded oriented submanifold) dari manifold yang lebih besar di mana bentuk didefinisikan
Lihat pula
[sunting | sunting sumber]Catatan kaki
[sunting | sunting sumber]- ^ Lebih tepatnya, teorema ini berkutat pada integral tertentu dengan limit atas variabel dan limit bawah sembarang. Jenis integral tertentu ini mengijinkan kita menghitung satu dari banyak antiturunan sebuah fungsi (kecuali untuk yang tidak nol). Oleh karena itu, ia hampir setara (ekuivalen) dengan integral tak tentu, didefinisikan oleh kebanyakan penulis sebagai sebuah operasi yang menghasilkan salah satu antiturunan sembarang sebuah fungsi, meliputi yang tidak nol.
- ^ Lihat Marlow Anderson, Victor J. Katz, Robin J. Wilson, Sherlock Holmes in Babylon and Other Tales of Mathematical History, Mathematical Association of America, 2004, hlm. 114.
- ^ Bers, Lipman. Calculus, hlm. 180–181 (Holt, Rinehart and Winston (1976).
Referensi
[sunting | sunting sumber]- Larson, Ron, Bruce H. Edwards, David E. Heyd. Calculus of a single variable. 7th ed. Boston: Houghton Mifflin Company, 2002.
- Leithold, L. (1996). The calculus 7 of a single variable. 6th ed. New York: HarperCollins College Publishers.
- Malet, A, Studies on James Gregorie (1638-1675) (PhD Thesis, Princeton, 1989).
- Stewart, J. (2003). Fundamental Theorem of Calculus. In Integrals. In Calculus: early transcendentals. Belmont, California: Thomson/Brooks/Cole.
- Turnbull, H W (ed.), The James Gregory Tercentenary Memorial Volume (London, 1939)
















![{\displaystyle [x,x+h]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6273c65efb7394e51a3d13a2575cac8b4f184a1b)



























![{\displaystyle {\begin{matrix}F(b)-F(a)&=&F(x_{n})\,+\,[-F(x_{n-1})\,+\,F(x_{n-1})]\,+\,\ldots \,+\,[-F(x_{1})+F(x_{1})]\,-\,F(x_{0})\,\\&=&[F(x_{n})\,-\,F(x_{n-1})]\,+\,[F(x_{n-1})\,+\,\ldots \,-\,F(x_{1})]\,+\,[F(x_{1})\,-\,F(x_{0})]\,.\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2fda47bf12b57e91f91c67e0c310fafe4f846db8)
![{\displaystyle F(b)-F(a)=\sum _{i=1}^{n}\,[F(x_{i})-F(x_{i-1})]\,.\qquad (1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f66b68a4db2bb6f252c3eb5e1e4f6bcdac310093)



![{\displaystyle F(b)-F(a)=\sum _{i=1}^{n}\,[F'(c_{i})(x_{i}-x_{i-1})]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/908e2bba9b00ee7a955e88122c76bd9be3d26d39)




![{\displaystyle F(b)-F(a)=\sum _{i=1}^{n}\,[f(c_{i})(\Delta x_{i})]\,.\qquad (2)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/94f81b337b19e5bfa63f7af16b49932bd741a128)


![{\displaystyle \lim _{\|\Delta \|\to 0}F(b)-F(a)=\lim _{\|\Delta \|\to 0}\sum _{i=1}^{n}\,[f(c_{i})(\Delta x_{i})]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b529d99855d23cb81925807978f33173449b08a)
![{\displaystyle F(b)-F(a)=\lim _{\|\Delta \|\to 0}\sum _{i=1}^{n}\,[f(c_{i})(\Delta x_{i})]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f54a9cbfa183b8c5e05f15d28302ee208a7c0c0a)
















