Frekuensi sudut

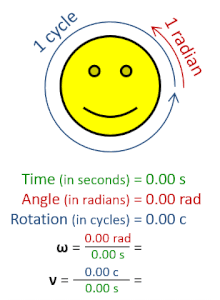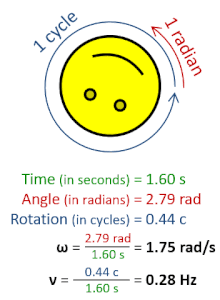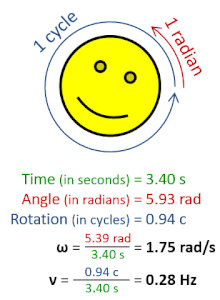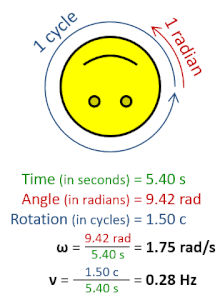
Bola berputar mengelilingi suatu sumbu. Titik yang lebih jauh dari sumbu bergerak lebih cepat, memenuhi ω=v/r.

Dalam fisika, frekuensi sudut ω adalah besaran skalar yang mengukur kecepatan putaran. Frekuensi sudut adalah perpindahan sudut per satuan waktu (dalam rotasi) atau kecepatan perubahan fase dari suatu gelombang sinusoidal (dalam oskilasi dan gelombang), atau sebagai kecepatan perubahan argumen dari fungsi sinus. Frekuensi sudut (atau kecepatan sudut) adalah besar dari besaran vektor kecepatan sudut. Istilah vektor frekuensi sudut ${\vec {\omega }}$ terkadang digunakan sebagai sinonim untuk besaran vektor kecepatan sudut.^[1]

Satu putaran sama dengan 2π radian, sehingga ^[1]^[2]

\omega ={{2\pi } \over T}={2\pi f},

dengan:

ω adalah frekuensi sudut atau kecepatan sudut (diukur dalam satuan radian per detik),

T adalah periode (diukur dalam satuan detik),

f adalah frekuensi biasa (diukur dalam satuan hertz) (terkadang dilambangkan dengan ν).

Satuan

Dalam satuan SI, frekuensi sudut biasanya diberikan dalam satuan radian per detik, termasuk ketika frekuensi sudutnya tidak berhubungan dengan suatu rotasi. Dari sudut pandang analisis dimensi, satuan Hertz (Hz) juga bisa digunakan, tetapi dalam praktiknya Hertz hanya digunakan untuk frekuensi bisa f, dan hampir tidak pernah digunakan untuk ω. Kebiasaan ini digunakan untuk membantu menghindari kebingungan^[3] yang bisa terjadi ketika mengerjakan masalah yang melibatkan frekuensi atau konstanta Planck karena satuan untuk sudut (putaran atau radian) tidak dituliskan dalam SI.^[4]^[5]^[6]^[7]^[8]

Contoh

Gerak melingkar

Pada benda yang mengalami gerak melingkar, terdapat suatu hubungan antara jari-jari atau jarak dari pusat ( $r$ ), kelajuan tangensial ( $v$ ), dan frekuensi sudut ( $\omega$ ). Dalam satu periode ( $T$ ), sebuah benda yang bergerak melingkar mengalami pergerakan sejauh $vT$ . Jarak ini sama dengan keliling dari jalur pergerakan melingkar benda tersebut, $2\pi r$ . Dengan menyamakan kedua persamaan ini, maka akan didapatkan rumus frekuensi sudut:

\omega =v/r.

Osilasi pegas

Benda yang dikaitkan pada pegas dapat mengalami osilasi. Apabila pegas tersebut diasumsikan ideal, tidak bermassa, dan tidak mengalami peredaman, maka pergerakan pegas merupakan gerakan harmonis dengan frekuensi sudut:^[9]

\omega ={\sqrt {\frac {k}{m}}},

dengan

k adalah konstanta pegas, dan

m adalah massa objek.

ω dinyatakan sebagai frekuensi natural (terkadang juga disimbolkan ω₀).

Ketika suatu benda mengalami osilasi, akselerasinya dapat dihitung menggunakan rumus

a=-\omega ^{2}x,

dengan x adalah perpindahan dari posisi setimbang. Rumus ini juga dapat dinyatakan sebagai:

a=-4\pi ^{2}f^{2}x.

Rangkaian LC

Frekuensi sudut resonansi dari suatu rangkaian LC sama dengan akar dari invers kapasitansi (C dalam satuan farad) dan induktansi rangkaian (L, dengan satuan henry):^[10]

\omega ={\sqrt {\frac {1}{LC}}}.

Referensi

^ ^a ^b Cummings, Karen; Halliday, David (2007). Understanding physics. New Delhi: John Wiley & Sons Inc., authorized reprint to Wiley – India. hlm. 449, 484, 485, 487. ISBN 978-81-265-0882-2. (UP1)
^ Holzner, Steven (2006). Physics for Dummies. Hoboken, New Jersey: Wiley Publishing Inc. hlm. 201. ISBN 978-0-7645-5433-9. angular frequency.
^ Lerner, Lawrence S. (1996-01-01). Physics for scientists and engineers. hlm. 145. ISBN 978-0-86720-479-7.
^ Mohr, J. C.; Phillips, W. D. (2015). "Dimensionless Units in the SI". Metrologia. 52 (1): 40–47. arXiv:1409.2794 . Bibcode:2015Metro..52...40M. doi:10.1088/0026-1394/52/1/40.
^ Mills, I. M. (2016). "On the units radian and cycle for the quantity plane angle". Metrologia. 53 (3): 991–997. Bibcode:2016Metro..53..991M. doi:10.1088/0026-1394/53/3/991.
^ "SI units need reform to avoid confusion". Editorial. Nature. 548 (7666): 135. 7 August 2011. doi:10.1038/548135b . PMID 28796224.
^ P. R. Bunker; I. M. Mills; Per Jensen (2019). "The Planck constant and its units". J Quant Spectrosc Radiat Transfer. 237: 106594. doi:10.1016/j.jqsrt.2019.106594.
^ P. R. Bunker; Per Jensen (2020). "The Planck constant of action $h$ _A". J Quant Spectrosc Radiat Transfer. 243: 106835. doi:10.1016/j.jqsrt.2020.106835.
^ Serway, Raymond A.; Jewett, John W. (2006). Principles of physics (edisi ke-4th). Belmont, CA: Brooks / Cole – Thomson Learning. hlm. 375, 376, 385, 397. ISBN 978-0-534-46479-0.
^ Nahvi, Mahmood; Edminister, Joseph (2003). Schaum's outline of theory and problems of electric circuits. McGraw-Hill Companies (McGraw-Hill Professional). hlm. 214, 216. ISBN 0-07-139307-2. Diarsipkan dari versi asli tanggal 2023-07-25. Diakses tanggal 2021-01-25. (LC1)

Bacaan terkait:

Olenick, Richard P.; Apostol, Tom M.; Goodstein, David L. (2007). The Mechanical Universe. New York City: Cambridge University Press. hlm. 383–385, 391–395. ISBN 978-0-521-71592-8. Diarsipkan dari versi asli tanggal 2023-07-25. Diakses tanggal 2020-07-19.

Pranala luar

Artikel bertopik fisika ini adalah sebuah rintisan. Anda dapat membantu Wikipedia dengan mengembangkannya.

[UP1-1] Cummings, Karen; Halliday, David (2007). Understanding physics. New Delhi: John Wiley & Sons Inc., authorized reprint to Wiley – India. hlm. 449, 484, 485, 487. ISBN 978-81-265-0882-2. (UP1)

[Holzner2O06-2] Holzner, Steven (2006). Physics for Dummies. Hoboken, New Jersey: Wiley Publishing Inc. hlm. 201. ISBN 978-0-7645-5433-9. angular frequency.

[Lerner1996-3] Lerner, Lawrence S. (1996-01-01). Physics for scientists and engineers. hlm. 145. ISBN 978-0-86720-479-7.

[Mohr2015-4] Mohr, J. C.; Phillips, W. D. (2015). "Dimensionless Units in the SI". Metrologia. 52 (1): 40–47. arXiv:1409.2794 . Bibcode:2015Metro..52...40M. doi:10.1088/0026-1394/52/1/40.

[Mills2016-5] Mills, I. M. (2016). "On the units radian and cycle for the quantity plane angle". Metrologia. 53 (3): 991–997. Bibcode:2016Metro..53..991M. doi:10.1088/0026-1394/53/3/991.

[Nature2011-6] "SI units need reform to avoid confusion". Editorial. Nature. 548 (7666): 135. 7 August 2011. doi:10.1038/548135b . PMID 28796224.

[Bunker2019-7] P. R. Bunker; I. M. Mills; Per Jensen (2019). "The Planck constant and its units". J Quant Spectrosc Radiat Transfer. 237: 106594. doi:10.1016/j.jqsrt.2019.106594.

[Bunker2020-8] P. R. Bunker; Per Jensen (2020). "The Planck constant of action $h$ _A". J Quant Spectrosc Radiat Transfer. 243: 106835. doi:10.1016/j.jqsrt.2020.106835.

[PoP1-9] Serway, Raymond A.; Jewett, John W. (2006). Principles of physics (edisi ke-4th). Belmont, CA: Brooks / Cole – Thomson Learning. hlm. 375, 376, 385, 397. ISBN 978-0-534-46479-0.

[LC1-10] Nahvi, Mahmood; Edminister, Joseph (2003). Schaum's outline of theory and problems of electric circuits. McGraw-Hill Companies (McGraw-Hill Professional). hlm. 214, 216. ISBN 0-07-139307-2. Diarsipkan dari versi asli tanggal 2023-07-25. Diakses tanggal 2021-01-25. (LC1)

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]