Algoritma tamak

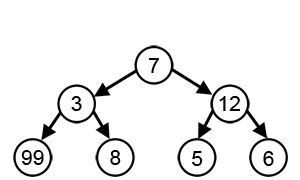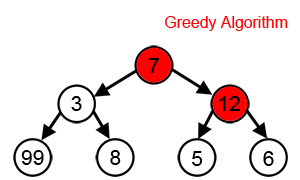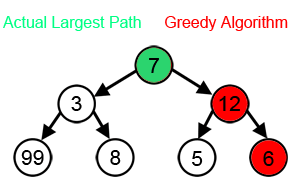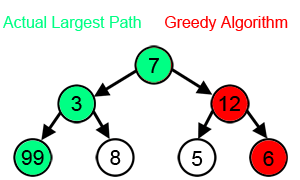
Algoritma tamak atau dalam bahasa Inggris greedy algorithm adalah algoritma apa pun yang mengikuti metode heuristik dalam pemecahan masalah untuk membuat pilihan optimal secara setempat di setiap tahap.^[1] Dalam banyak permasalahan, strategi tamak tidak menghasilkan solusi optimal, tetapi suatu heuristik tamak dapat menghasilkan solusi optimal lokal yang mendekati solusi optimal global dalam jangka waktu yang wajar.

Misalnya, strategi tamak untuk masalah penjual keliling (yang memiliki kerumitan komputasi tinggi) adalah heuristik berikut: "Pada setiap langkah perjalanan, kunjungi kota terdekat yang belum dikunjungi." Heuristik ini tidak bertujuan untuk menemukan solusi terbaik, tetapi ia berakhir dalam sejumlah langkah yang wajar. Yang mana menemukan solusi optimal untuk masalah yang kompleks biasanya memerlukan banyak langkah yang tak masuk akal. Dalam optimasi matematis, algoritma tamak secara optimal dapat menyelesaikan masalah kombinatorial yang memiliki sifat matroid dan memberikan hampiran faktor konstan untuk masalah optimasi dengan struktur submodular.

Spesifik

Algoritme tamak menghasilkan solusi yang baik pada beberapa masalah matematis, tetapi tidak pada masalah lainnya. Sebagian besar masalah yang algoritma greedy kerjakan memiliki dua properti:

Properti pemilihan tamak: Kita dapat membuat pilihan apa pun yang tampaknya terbaik saat ini dan kemudian menyelesaikan sub-masalah yang muncul kemudian. Pilihan yang dibuat oleh algoritma tamak mungkin bergantung pada pilihan yang dibuat sejauh ini, tetapi tidak pada pilihan masa depan atau semua solusi terhadap submasalah. Ini secara berulang-ulang membuat pilihan tamak satu demi satu, mengurangi setiap masalah menjadi masalah yang lebih kecil. Dengan kata lain, algoritma tamak tidak pernah mempertimbangkan kembali pilihannya. Inilah perbedaan utamanya dengan pemrograman dinamis yang bersifat menyeluruh dan menjamin untuk menemukan solusinya. Setelah setiap tahap selesai, pemrograman dinamis membuat keputusan berdasarkan semua keputusan yang dibuat pada tahap sebelumnya dan dapat mempertimbangkan kembali jalur algoritmik tahap sebelumnya menuju solusi.
Substruktur optimal: “Suatu masalah menunjukkan substruktur optimal jika solusi optimal terhadap masalah tersebut mengandung solusi optimal terhadap sub-masalah.” ^[2]

Kasus kegagalan

Contoh kejadian tentang bagaimana algoritma tamak dapat gagal mencapai solusi optimal.

Dimulai dari A, algoritma tamak yang mencoba menemukan nilai maksimum dengan mengikuti kemiringan terbesar akan menemukan maksimum lokal di "m", tanpa menyadari maksimum global di "M".

Untuk mencapai nilai terbesar, pada setiap langkah, algoritma tamak akan memilih apa yang tampak sebagai pilihan langsung yang optimal, sehingga ia akan memilih 12 dan bukannya 3 pada langkah kedua, dan tidak akan mencapai solusi terbaik, yaitu 99.

Algoritme tamak gagal menghasilkan solusi optimal untuk banyak masalah lain dan bahkan mungkin menghasilkan solusi unik yang paling buruk . Salah satu contohnya adalah masalah travelling salesman yang disebutkan di atas: untuk setiap jumlah kota, terdapat penetapan jarak antar kota dimana heuristik tetangga terdekat menghasilkan tur terburuk yang mungkin terjadi.^[3] Untuk kemungkinan contoh lainnya, lihat efek cakrawala.

Jenis

Algoritme tamak dapat dikategorikan sebagai algoritma yang 'berpandangan sempit', dan juga 'tidak dapat dipulihkan'. Algoritma ini hanya ideal untuk permasalahan yang memiliki 'substruktur optimal'. Meskipun demikian, untuk banyak masalah sederhana, algoritma yang paling cocok adalah algoritma tamak. Namun, penting untuk dicatat bahwa algoritma tamak dapat digunakan sebagai algoritma seleksi untuk mengutamakan pilihan dalam pencarian, atau algoritma cabang-daan-batas. Ada beberapa variasi pada algoritma tamak:

Algoritma tamak murni
Algoritma tamak ortogonal
Algoritme tamak santai

Teori

Algoritma tamak memiliki sejarah panjang dalam studi optimasi kombinatorial dan ilmu komputer teoretis. Heuristik tamak diketahui memberikan hasil yang kurang optimal pada banyak masalah,^[4] sehingga pertanyaan yang wajar adalah:

Untuk masalah apa algoritma tamak bekerja secara optimal?
Untuk masalah manakah algoritma tamak menjamin solusi yang sekiranya optimal?
Untuk permasalahan manakah algoritma tamak dijamin tidak akan menghasilkan solusi optimal?

Sejumlah besar sastra menjawab pertanyaan-pertanyaan ini untuk kelas masalah umum, seperti matroid, serta untuk masalah khusus, seperti <i>set cover</i>.

Matroid

Matroid adalah struktur matematika yang menggeneralisasi konsep independensi linier dari ruang vektor ke himpunan sembarang. Jika suatu masalah optimasi mempunyai struktur matroid, maka algoritma tamak yang sesuai akan dapat menyelesaikannya secara optimal.^[5]

Fungsi submodular

Sebuah fungsi $f$ didefinisikan pada himpunan bagian dari suatu himpunan $\Omega$ disebut submodular, jika untuk setiap $S,T\subseteq \Omega$ kita mempunyai $f(S)+f(T)\geq f(S\cup T)+f(S\cap T)$ .

Misalkan seseorang ingin mencari sebuah himpunan $S$ yang memaksimalkan $f$ . Algoritma tamak, yang membangun satu himpunan $S$ dengan menambahkan elemen secara bertahap yang meningkatkan $f$ paling banyak pada setiap langkah, menghasilkan keluaran sebuah himpunan yang paling sedikit $(1-1/e)\max _{X\subseteq \Omega }f(X)$ .^[6] Artinya, ketamakan bermain dalam faktor konstan $(1-1/e)\approx 0.63$ sama baiknya dengan solusi optimal.

Jaminan serupa dapat dibuktikan ketika kendala tambahan, seperti batasan kardinalitas, ^[7] diterapkan pada keluaran. Meskipun sering kali diperlukan sedikit variasi pada algoritma tamak. Lihat^[8] untuk ikhtisarnya.

Masalah lain dengan penjaminan

Masalah lain yang mana algoritma tamak memberikan jaminan yang kuat, tetapi bukan solusi optimal, termasuk

Banyak dari permasalahan ini memiliki batas bawah yang sesuai, yaitu algoritma tamak tidak berkinerja lebih baik daripada jaminan dalam kasus terburuk.

Pemberlakuan

Algoritme tamak biasanya (tetapi tidak selalu) gagal menemukan solusi optimal secara global karena algoritma tersebut biasanya tidak beroperasi secara mendalam pada semua data. Algoritma jenis ini dapat membuat komitmen pada pilihan-pilihan tertentu terlalu dini, sehingga mencegah mereka untuk menemukan solusi terbaik secara keseluruhan nantinya. Misalnya, semua algoritma pewarnaan tamak yang diketahui untuk masalah pewarnaan graf dan semua masalah NP-lengkap lainnya tidak secara konsisten menemukan solusi optimal. Namun, algoritma jenis ini berguna karena mereka cepat berpikir dan sering memberikan hampiran yang baik secara optimal.

Jika algoritma tamak dapat dibuktikan menghasilkan optimal global untuk kelas masalah tertentu, biasanya algoritma ini menjadi metode pilihan karena lebih cepat dibandingkan metode optimasi lain seperti pemrograman dinamis. Contoh algoritma tamak tersebut adalah algoritma Kruskal dan algoritma Prim untuk mencari pohon rentang minimum serta algoritma untuk mencari pohon Huffman optimal.

Algoritmq tamak juga muncul di perutean jaringan. Dengan menggunakan perutean tamak, sebuah pesan diteruskan ke simpul tetangga “terdekat” dengan tujuan. Gagasan tentang lokasi sebuah simpul (dan karenanya "kedekatan") dapat ditentukan oleh lokasi fisiknya, seperti dalam perutean geografis yang digunakan oleh jaringan ad hoc . Lokasi mungkin juga merupakan konstruksi buatan seperti dalam perutean dunia kecil dan tabel hash beredar.

Contoh

Masalah pemilihan kegiatan merupakan ciri khasnya kelas masalah ini, yang tujuannya adalah memilih kegiatan sebanyak-banyaknya yang tidak berbenturan.
Dalam permainan komputer Macintosh Crystal Quest tujuannya adalah mengumpulkan kristal, dengan cara yang mirip dengan masalah penjual keliling . Permainan ini memiliki mode demo yang menggunakan algoritma tamak untuk mencapai setiap kristal. Kecerdasan buatan tidak memperhitungkan hambatan, sehingga mode demo sering kali berakhir dengan cepat.
Pengejaran pencocokan adalah contoh algoritma tamak yang diterapkan pada hampiran sinyal.
Algoritma tamak menemukan solusi optimal untuk masalah Malfatti dalam menemukan tiga lingkaran yang berlepasan dalam suatu segitiga yang memaksimalkan luas total lingkaran; diperkirakan bahwa algoritma tamak yang sama optimal untuk lingkaran dengan jumlah berapapun.
Algoritma tamak digunakan untuk membangun pohon Huffman dalampengkodean Huffman yang algoritma ini menemukan solusi optimal.
Dalam pemelajaran pohon keputusan, algoritma tamak sering digunakan, tetapi tidak ada jaminan ditemukannya solusi optimal.
- Salah satu algoritma yang populer adalah algoritma ID3 untuk konstruksi pohon keputusan.
Algoritma Dijkstra dan algoritma pencarian A* merupakan algoritma tamak yang optimal untuk traversal graf dan pencarian lintasan terpendek.
- Pencarian A* optimal secara kondisional, memerlukan "heuristik yang dapat diterima" yang tidak akan melebih-lebihkan biaya lintasan.
Algoritma Kruskal dan algoritma Prim adalah algoritma tamak untuk membangun pohon rentang minimum dari suatu graf terhubung tertentu. Algoritma ini selalu menemukan solusi optimal, yang mungkin tidak unik secara umum.
Algoritma Sequitur dan Lempel-Ziv-Welch merupakan algoritma tamak untuk induksi tata bahasa .

Lihat pula

Referensi

^ Black, Paul E. (2 February 2005). "greedy algorithm". Dictionary of Algorithms and Data Structures. U.S. National Institute of Standards and Technology (NIST). Diakses tanggal 17 August 2012.
^ Cormen et al. 2001
^ Gutin, Gregory; Yeo, Anders; Zverovich, Alexey (2002). "Traveling salesman should not be greedy: Domination analysis of greedy-type heuristics for the TSP". Discrete Applied Mathematics. 117 (1–3): 81–86. doi:10.1016/S0166-218X(01)00195-0.
^ Feige 1998
^ Papadimitriou & Steiglitz 1998
^ Nemhauser, Wolsey & Fisher 1978
^ Buchbinder et al. 2014
^ Krause & Golovin 2014
^ "Lecture 5: Introduction to Approximation Algorithms" (PDF). Advanced Algorithms (2IL45) — Course Notes. TU Eindhoven. Diarsipkan dari versi asli (PDF) tanggal 2022-10-09.

Sumber

Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001). "16 Greedy Algorithms". Introduction To Algorithms. MIT Press. hlm. 370–. ISBN 978-0-262-03293-3.
Gutin, Gregory; Yeo, Anders; Zverovich, Alexey (2002). "Traveling salesman should not be greedy: Domination analysis of greedy-type heuristics for the TSP". Discrete Applied Mathematics. 117 (1–3): 81–86. doi:10.1016/S0166-218X(01)00195-0 .
Bang-Jensen, Jørgen; Gutin, Gregory; Yeo, Anders (2004). "When the greedy algorithm fails". Discrete Optimization. 1 (2): 121–127. doi:10.1016/j.disopt.2004.03.007 .
Bendall, Gareth; Margot, François (2006). "Greedy-type resistance of combinatorial problems". Discrete Optimization. 3 (4): 288–298. doi:10.1016/j.disopt.2006.03.001 .
Feige, U. (1998). "A threshold of ln n for approximating set cover" (PDF). Journal of the ACM. 45 (4): 634–652. doi:10.1145/285055.285059. Diarsipkan dari versi asli (PDF) tanggal 2022-10-09.
Nemhauser, G.; Wolsey, L.A.; Fisher, M.L. (1978). "An analysis of approximations for maximizing submodular set functions—I". Mathematical Programming. 14 (1): 265–294. doi:10.1007/BF01588971.
Buchbinder, Niv; Feldman, Moran; Naor, Joseph (Seffi); Schwartz, Roy (2014). "Submodular maximization with cardinality constraints" (PDF). Proceedings of the twenty-fifth annual ACM-SIAM symposium on Discrete algorithms. Society for Industrial and Applied Mathematics. doi:10.1137/1.9781611973402.106. ISBN 978-1-61197-340-2. Diarsipkan dari versi asli (PDF) tanggal 2022-10-09.
Krause, A.; Golovin, D. (2014). "Submodular Function Maximization". Dalam Bordeaux, L.; Hamadi, Y.; Kohli, P. Tractability: Practical Approaches to Hard Problems. Cambridge University Press. hlm. 71–104. doi:10.1017/CBO9781139177801.004. ISBN 9781139177801.
Papadimitriou, Christos H.; Steiglitz, Kenneth (1998). Combinatorial Optimization: Algorithms and Complexity. Dover.

Pranala luar

Hazewinkel, Michiel, ed. (2001) [1994], "Greedy algorithm", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4
Gift, Noah. "Contoh koin greedy dalam bahasa Python".

[NISTg-1] Black, Paul E. (2 February 2005). "greedy algorithm". Dictionary of Algorithms and Data Structures. U.S. National Institute of Standards and Technology (NIST). Diakses tanggal 17 August 2012.

[2] Cormen et al. 2001

[3] Gutin, Gregory; Yeo, Anders; Zverovich, Alexey (2002). "Traveling salesman should not be greedy: Domination analysis of greedy-type heuristics for the TSP". Discrete Applied Mathematics. 117 (1–3): 81–86. doi:10.1016/S0166-218X(01)00195-0.

[4] Feige 1998

[5] Papadimitriou & Steiglitz 1998

[6] Nemhauser, Wolsey & Fisher 1978

[7] Buchbinder et al. 2014

[8] Krause & Golovin 2014

[9] "Lecture 5: Introduction to Approximation Algorithms" (PDF). Advanced Algorithms (2IL45) — Course Notes. TU Eindhoven. Diarsipkan dari versi asli (PDF) tanggal 2022-10-09.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]