Fungsi phi Euler
Artikel atau sebagian dari artikel ini mungkin diterjemahkan dari Fungsi phi Euler di en.wikipedia.org. Isinya masih belum akurat, karena bagian yang diterjemahkan masih perlu diperhalus dan disempurnakan. Jika Anda menguasai bahasa aslinya, harap pertimbangkan untuk menelusuri referensinya dan menyempurnakan terjemahan ini. Anda juga dapat ikut bergotong royong pada ProyekWiki Perbaikan Terjemahan. (Pesan ini dapat dihapus jika terjemahan dirasa sudah cukup tepat. Lihat pula: panduan penerjemahan artikel) |

Dalam teori bilangan, fungsi phi Euler (bahasa Inggris: Euler's totient function) adalah fungsi yang menghitung bilangan bulat positif hingga diberikan bilangan bulat yang prima nisbi dengan . Fungsi ini ditulis dengan menggunakan huruf Yunani, phi, yang dilambangkan sebagai atau menyatakan kardinal himpunan bilangan asli dimana .
Bilangan bulat positif yang < 9 adalah 1, 2, 3, 4, 5, 6, 7, 8. Diantara bilangan-bilangan tersebut yang saling prima terhadap 9 adalah 1, 2, 4, 5, 7, 8, maka banyaknya bilangan yang saling prima terhadap 9 adalah sebanyak 6 sehingga φ(9) = 6.
Fungsi ini dikemukakan oleh Leonhard Euler (L. 15 April 1707, Swiss. w. 18 September 1783, Rusia).
Identitas
[sunting | sunting sumber]Terdapat beberapa identitas mengenai fungsi Euler phi, diantaranya:
- ,
- , untuk adalah bilangan prima
- jika
Rumus lainnya
[sunting | sunting sumber]Apabila rumus lain mengenai fungsi Euler phi, diantaranya
- , untuk setiap
- Perhatikan kasus khusus
- Bandingkan dengan rumus
- (Lihat kelipatan persekutuan terkecil.)
- φ(n) genap untuk n ≥ 3. Selain itu, jika n memiliki r faktor prima ganjil yang berbeda, 2r | φ(n)
- Untuk a > 1 dan n > 6 sehingga 4 ∤ n terdapat l ≥ 2n sedemikian sehingga l | φ(an − 1).
- di mana adalah radikal dari .
- (dengan adalah konstanta Euler–Mascheroni).
- dimana adalah bilangan bulat positif dan adalah jumlah faktor prima yang berbeda dari .[6]
Beberapa bilangan
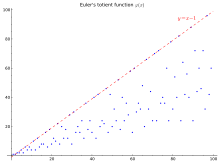
[sunting | sunting sumber]100 nilai pertama (barisan A000010 pada OEIS) ditampilkan pada tabel dan grafik di bawah ini:
untuk + 1 2 3 4 5 6 7 8 9 10 0 1 1 2 2 4 2 6 4 6 4 10 10 4 12 6 8 8 16 6 18 8 20 12 10 22 8 20 12 18 12 28 8 30 30 16 20 16 24 12 36 18 24 16 40 40 12 42 20 24 22 46 16 42 20 50 32 24 52 18 40 24 36 28 58 16 60 60 30 36 32 48 20 66 32 44 24 70 70 24 72 36 40 36 60 24 78 32 80 54 40 82 24 64 42 56 40 88 24 90 72 44 60 46 72 32 96 42 60 40
Dalam grafik di kanan atas baris adalah batas atas valid untuk semua selain satu, dan dicapai jika dan hanya jika adalah bilangan prima. Batas bawah sederhana adalah , yang agak longgar: sebenarnya, lower limit dari grafik sebanding dengan .[7]
Fungsi pembangkit
[sunting | sunting sumber]Deret Dirichlet untuk dapat ditulis dalam istilah fungsi zeta Riemann sebagai:[8]
Fungsi pembangkit deret Lambert adalah[9]
konvergen untuk .
Keduanya dibuktikan dengan manipulasi deret dasar dan rumus untuk .
Rasio bilangan berurutan
[sunting | sunting sumber]Pada tahun 1950 Somayajulu membuktikan[10][11]
- dan
Pada tahun 1954 Schinzel dan Sierpiński memperkuat ini, membuktikan[10][11] bahwa himpunan
adalah padat dalam bilangan riil positif. Mereka pun membuktikannya[10] bahwa himpunan
padat dalam interval .
Lihat pula
[sunting | sunting sumber]- Fungsi Carmichael
- Konjektur Duffin–Schaeffer
- Generalisasi teorema kecil Fermat
- Bilangan komposit tinggi
- Grup perkalian bilangan bulat modulo n
- Jumlah Ramanujan
- Fungsi penjumlahan total
Catatan
[sunting | sunting sumber]- ^ "Euler's totient function". Khan Academy. Diakses tanggal 2016-02-26.
- ^ Dineva (dalam referensi eksternal), prop. 1
- ^ a b Walfisz, Arnold (1963). Weylsche Exponentialsummen in der neueren Zahlentheorie. Mathematische Forschungsberichte (dalam bahasa Jerman). 16. Berlin: VEB Deutscher Verlag der Wissenschaften. Zbl 0146.06003.
- ^ Lomadse, G., "The scientific work of Arnold Walfisz" (PDF), Acta Arithmetica, 10 (3): 227–237, diarsipkan (PDF) dari versi asli tanggal 2023-06-06, diakses tanggal 2020-04-22
- ^ a b Sitaramachandrarao, R. (1985). "On an error term of Landau II". Rocky Mountain J. Math. 15: 579–588.
- ^ Bordellès di pranala luar
- ^ Kesalahan pengutipan: Tag
<ref>tidak sah; tidak ditemukan teks untuk ref bernamahw328 - ^ Hardy & Wright 1979, thm. 288
- ^ Hardy & Wright 1979, thm. 309
- ^ a b c Ribenboim, p.38
- ^ a b Sándor, Mitrinović & Crstici (2006) p.16
Referensi
[sunting | sunting sumber]Disquisitiones Arithmeticae telah diterjemahkan dari bahasa Latin ke dalam bahasa Inggris dan Jerman. Edisi Jerman mencakup semua makalah Gauss tentang teori bilangan: semua bukti timbal balik kuadrat, penentuan tanda jumlah Gauss, penyelidikan timbal balik biquadratic, dan catatan yang tidak diterbitkan.
Referensi ke Disquisitiones adalah dari bentuk Gauss, DA, art. nnn.
- Abramowitz, M.; Stegun, I. A. (1964), Handbook of Mathematical Functions, New York: Dover Publications, ISBN 0-486-61272-4. See paragraph 24.3.2.
- Bach, Eric; Shallit, Jeffrey (1996), Algorithmic Number Theory (Vol I: Efficient Algorithms), MIT Press Series in the Foundations of Computing, Cambridge, MA: The MIT Press, ISBN 0-262-02405-5, Zbl 0873.11070
- Dickson, Leonard Eugene, "History Of The Theory Of Numbers", vol 1, chapter 5 "Euler's Function, Generalizations; Farey Series", Chelsea Publishing 1952
- Ford, Kevin (1999), "The number of solutions of φ(x) = m", Annals of Mathematics, 150 (1): 283–311, doi:10.2307/121103, ISSN 0003-486X, JSTOR 121103, MR 1715326, Zbl 0978.11053.
- Gauss, Carl Friedrich; Clarke, Arthur A. (translator into English) (1986), Disquisitiones Arithmeticae (Second, corrected edition), New York: Springer, ISBN 0-387-96254-9
- Gauss, Carl Friedrich; Maser, H. (translator into German) (1965), Untersuchungen uber hohere Arithmetik (Disquisitiones Arithmeticae & other papers on number theory) (Second edition), New York: Chelsea, ISBN 0-8284-0191-8
- Graham, Ronald; Knuth, Donald; Patashnik, Oren (1994), Concrete Mathematics: a foundation for computer science (edisi ke-2nd), Reading, MA: Addison-Wesley, ISBN 0-201-55802-5, Zbl 0836.00001
- Guy, Richard K. (2004), Unsolved Problems in Number Theory, Problem Books in Mathematics (edisi ke-3rd), New York, NY: Springer-Verlag, ISBN 0-387-20860-7, Zbl 1058.11001
- Hardy, G. H.; Wright, E. M. (1979), An Introduction to the Theory of Numbers (edisi ke-Fifth), Oxford: Oxford University Press, ISBN 978-0-19-853171-5
- Long, Calvin T. (1972), Elementary Introduction to Number Theory (edisi ke-2nd), Lexington: D. C. Heath and Company, LCCN 77-171950
- Pettofrezzo, Anthony J.; Byrkit, Donald R. (1970), Elements of Number Theory, Englewood Cliffs: Prentice Hall, LCCN 77-81766
- Ribenboim, Paulo (1996), The New Book of Prime Number Records (edisi ke-3rd), New York: Springer, ISBN 0-387-94457-5, Zbl 0856.11001
- Sandifer, Charles (2007), The early mathematics of Leonhard Euler, MAA, ISBN 0-88385-559-3
- Sándor, József; Mitrinović, Dragoslav S.; Crstici, Borislav, ed. (2006), Handbook of number theory I, Dordrecht: Springer-Verlag, hlm. 9–36, ISBN 1-4020-4215-9, Zbl 1151.11300
- Sándor, Jozsef; Crstici, Borislav (2004). Handbook of number theory II
 . Dordrecht: Kluwer Academic. hlm. 179–327. ISBN 1-4020-2546-7. Zbl 1079.11001.
. Dordrecht: Kluwer Academic. hlm. 179–327. ISBN 1-4020-2546-7. Zbl 1079.11001. - Schramm, Wolfgang (2008), "The Fourier transform of functions of the greatest common divisor", Electronic Journal of Combinatorial Number Theory, A50 (8(1)), diarsipkan dari versi asli tanggal 2009-05-01, diakses tanggal 2021-01-27.
Pranala luar
[sunting | sunting sumber]- Hazewinkel, Michiel, ed. (2001) [1994], "Totient function", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4
- Euler's Phi Function and the Chinese Remainder Theorem — proof that φ(n) is multiplicative Diarsipkan 2021-02-28 di Wayback Machine.
- Euler's totient function calculator in JavaScript — up to 20 digits Diarsipkan 2023-07-06 di Wayback Machine.
- Dineva, Rosica, The Euler Totient, the Möbius, and the Divisor Functions Diarsipkan 2021-01-16 di Wayback Machine.
- Plytage, Loomis, Polhill Summing Up The Euler Phi Function Diarsipkan 2023-05-23 di Wayback Machine.















































