Morfologi matematis

Sebuah bentuk (biru) serta dilatasi (hijau) dan erosinya (kuning) dengan elemen penyusun berbentuk belah ketupat.

Morfologi matematis (MM) adalah teori dan teknik analisis dan pengolahan struktur geometri yang berdasarkan teori himpunan, teori kekisi, topologi, dan fungsi acak. MM sering dipakai dalam gambar digital, tetapi juga bisa dipakai dalam graf, jala poligon, padatan, dan struktur spasial lainnya.

Konsep ruang malar topologis dan geometris, seperti ukuran, bentuk, kecembungan, keterhubungan, dan jarak geodesi, diperkenalkan oleh MM dalam ruang kontinu ataupun ruang diskret. MM juga menjadi dasar pengolahan citra morfologis yang terdiri dari himpunan operator yang mengubah citra sesuai sifat-sifat tertentu.

Yang termasuk operasi morfologis dasar antara lain erosi, dilasi, pembukaan, dan penutupan.

Pada awalnya, MM dikembangkan untuk citra biner, lalu diperluas ke fungsi dan citra berderajat keabuan.

Morfologi biner

Dalam morfologi biner, sebuah citra dilihat sebagai himpunan bagian dari ruang Euklides $\mathbb {R} ^{d}$ atau kekisi bilangan bulat $\mathbb {Z} ^{d}$ untuk dimensi d.

Elemen penyusun

Konsep dasar morfologi biner adalah untuk menyelidiki citra dengan bentuk sederhana yang telah ditentukan, lalu menyimpulkan apakah bentuk tersebut cocok atau tidak terhadap citra. Penyelidik sederhana ini disebut dengan elemen penyusun dan berupa citra biner juga, yaitu himpunan bagian dari ruang atau kekisinya.

Berikut contoh elemen penyusun yang jamak dipakai (dinyatakan sebagai B dalam E).

• Misal $E=\mathbb {R} ^{2}$; B adalah lingkaran berjari-jari r dan berpusat di titik asal.
• Misal $E=\mathbb {Z} ^{2}$; B adalah persegi 3 × 3, yaitu B = {(−1, −1), (−1, 0), (−1, 1), (0, −1), (0, 0), (0, 1), (1, −1), (1, 0), (1, 1)}.
• Misal $E=\mathbb {Z} ^{2}$; B adalah bentuk palang, yaitu B = {(−1, 0), (0, −1), (0, 0), (0, 1), (1, 0)}.

Operasi dasar

Operasi dasarnya tidak terpengaruh pergeseran (translasi).

Misalkan E adalah ruang Euklides dan A adalah citra biner dalam E.

Erosi

Erosi kotak biru gelap oleh sebuah lingkaran menghasilkan kotak biru terang.

Erosi citra biner A dengan elemen penyusun B didefinisikan sebagai berikut:

$A\ominus B=\{z\in E\mid B_{z}\subseteq A\}$

dengan B_z adalah pergeseran B oleh z, yaitu $B_{z}=\{b+z\mid b\in B\}$, dan $\forall z\in E$.

Erosi A oleh B juga bisa dinyatakan sebagai $A\ominus B=\bigcap _{b\in B}A_{-b}$.

Contoh penggunaan: Misalkan kita menerima faks berupa fotokopi gelap. Semuanya tampak seperti ditulis dengan pena yang bocor. Proses erosi akan menipiskan garis yang terlalu tebal sehingga menjadi garis tipis dan memunculkan lubang dalam huruf "o".

Dilasi

Dilasi kotak biru gelap oleh sebuah lingkaran menghasilkan kotak biru terang.

Dilasi citra biner A oleh elemen penyusun B didefinisikan sebagai berikut.

$A\oplus B=\bigcup _{b\in B}A_{b}.$

Dilasi bersifat komutatif sehingga berlaku $A\oplus B=B\oplus A=\bigcup _{a\in A}B_{a}$.

Contoh penggunaan: Dilasi adalah kebalikan dari erosi. Bentuk yang digambar dengan tipis akan menjadi tebal. Tulisan yang ditulis menjadi tebal seperti pena yang bocor.

Pembukaan

Pembukaan kotak biru gelap oleh sebuah lingkaran menghasilkan kotak biru terang dengan sudut yang melingkar.

Pembukaan citra biner A oleh B didapatkan dari erosi A oleh B, lalu diikuti dengan dilasi oleh B.

$A\circ B=(A\ominus B)\oplus B$

Contoh penggunaan: Misalkan ada tulisan pada kertas yang kurang menyerap sehingga tulisannya seperti memiliki rambut. Pembukaan ini menghilangkan rambut-rambut kecil itu. Efek sampingnya adalah semua bentuk menjadi tumpul. Sudut-sudut yang tajam mulai menghilang.

Penutupan

Penutupan bentuk warna biru gelap (gabungan dua persegi) oleh sebuah lingkaran menghasilkan gabungan bentuk biru gelap dan biru terang.

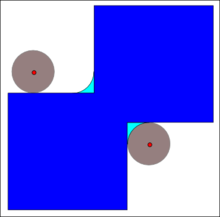
Penutupan A oleh B didapatkan dari dilasi A oleh B, lalu diikuti dengan erosi oleh B.

$A\bullet B=(A\oplus B)\ominus B$

Daftar pustaka

• Jean Serra (1982). Image Analysis and Mathematical Morphology. ISBN 0-1263-7240-3. 
• Jean Serra (1988). Image Analysis and Mathematical Morphology Volume 2: Theoretical Advances. ISBN 0-1263-7241-1. 
• Edward R. Dougherty (1992). An Introduction to Morphological Image Processing. ISBN 0-8194-0845-X. 
• Pierre Soille (2003). Morphological Image Analysis; Principles and Applications (edisi ke-2). ISBN 3-5406-5671-5. 
• J. Serra dan Ph. Salembier, ed. (1993). "Mathematical Morphology and its Application to Signal Processing". Proceedings of the 1st International Workshop on Mathematical Morphology and Its Applications to Signal Processing (ISMM '93). ISBN 8-4765-3271-7. Pemeliharaan CS1: Menggunakan parameter penyunting (link)
• J. Serra dan P. Soille, ed. (1994). "Mathematical Morphology and Its Applications to Image Processing". Proceedings of the 2nd International Symposium on Mathematical Morphology (ISMM '94). ISBN 0-7923-3093-5. Pemeliharaan CS1: Menggunakan parameter penyunting (link)
• Henk J. A. M. Heijmans dan Jos B. T. M. Roerdink, ed. (1998). "Mathematical Morphology and its Applications to Image and Signal Processing". Proceedings of the 4th International Symposium on Mathematical Morphology (ISMM '98). ISBN 0-7923-5133-9. Pemeliharaan CS1: Menggunakan parameter penyunting (link)
• Christian Ronse, Laurent Najman, dan Etienne Decencière, ed. (2005). Mathematical Morphology: 40 Years On. ISBN 1-4020-3442-3. Pemeliharaan CS1: Menggunakan parameter penyunting (link)
• Gerald J. F. Banon, Junior Barrera, dan Ulisses M. Braga-Neto, ed. (2007). "Mathematical Morphology and its Applications to Signal and Image Processing". Proceedings of the 8th International Symposium on Mathematical Morphology (ISMM '07). ISBN 978-8-5170-0032-4. Pemeliharaan CS1: Menggunakan parameter penyunting (link)
• Laurent Najman dan Hugues Talbot, ed. (2010). Mathematical Morphology: from Theory to Applications. ISTE-Wiley. ISBN 978-1-8482-1215-2. Pemeliharaan CS1: Menggunakan parameter penyunting (link)