Paradoks hotel Hilbert

Paradoks Hotel Hilbert (bahasa percakapan: Paradoks Hotel Takhingga atau Hotel Hilbert) adalah suatu eksperimen pikiran yang mengilustrasikan sifat kontraintuitif dari himpunan-himpunan takhingga, yaitu sebuah hotel yang dengan jumlah kamar yang tak terhingga dan telah terisi penuh masih dapat menampung tamu-tamu tambahan, bahkan takhingga banyaknya, dan proses ini dapat dilakukan berulang-ulang. Gagasan ini diperkenalkan oleh David Hilbert pada kuliah tahun 1925 "Über das Unendliche", dicetak ulang pada (Hilbert 2013, p.730), dan dipopulerkan melalui buku tahun 1947 One Two Three... Infinity karya George Gamow.^[1]^[2]

Isi paradoks

Hilbert membayangkan suatu hotel khayalan dengan kamar yang diberi nomor $1$ , $2$ , $3$ , dan seterusnya, tanpa batas atas. Hal ini disebut sebagai terhitung takhingga banyaknya kamar. Pada awalnya, setiap kamar telah terisi penuh, dan kemudian beberapa tamu baru pun berdatangan, masing-masing mengharapkan sebuah kamarnya. Sebuah hotel normal (dengan jumlah kamar yang terbatas) tidak dapat menampung tamu baru setelah semua kamar telah terisi penuh. Akan tetapi, dapat ditunjukkan bahwa para tamu yang sudah ada dan para pendatang baru — bahkan dalam jumlah yang tak terhingga — dapat memiliki kamar masing-masing di hotel takhingga.

Beberapa pendatang baru

Dengan satu pendatang tambahan, hotel takhingga ini dapat menampung pendatang tersebut beserta semua tamu yang sudah ada jika takhingga banyaknya tamu pindah kamar secara bersamaan. Tamu yang semula menghuni kamar nomor $1$ dipindahkan ke kamar nomor $2$ , Tamu yang semula menghuni kamar nomor $2$ dipindahkan ke kamar nomor $3$ , dan seterusnya. Secara umum, setiap tamu pindah dari kamar nomor $n$ ke kamar nomor $n+1$ .

Hotel takhingga tidak memiliki kamar terakhir, sehingga target kamar dari setiap tamu dijamin ada dan tidak ada tamu yang perlu diusir. Setelah proses pemindahan kamarnya selesai, tidak ada yang menghuni kamar nomor $1$ , sehingga pendatang tambahan tadi dapat menempati kamar tersebut. Secara umum, jika terdapat $k$ pendatang tambahan, pihak hotel dapat menerapkan prosedur serupa dengan memindahkan setiap tamu dari kamar $n$ ke kamar $n+k$ .

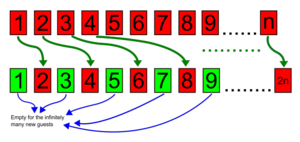
Takhingga banyaknya pendatang baru

Hotel takhingga ini juga mungkin untuk mengakomodasi terhitung takhingga banyaknya pendatang baru: cukup pindahkan tamu yang awalnya menempati kamar nomor $1$ ke kamar nomor $2$ , tamu yang awalnya menempati kamar nomor $2$ ke kamar nomor $4$ , tamu yang awalnya menempati kamar nomor $3$ ke kamar nomor $6$ , dan secara umum, tamu yang awalnya menempati kamar $n$ dipindahkan ke kamar $2n$ (2 dikali $n$ ), dan semua kamar bernomor ganjil (yang merupakan himpunan terhitung takhingga) akan menjadi kosong dan siap ditempati oleh para pendatang baru.

Takhingga banyaknya bus yang berisi penumpang yang takhingga banyaknya

Hotel takhingga ini dapat mengakomodasi terhitung takhingga banyaknya bus besar yang masing-masing mengangkut terhitung banyaknya penumpang, melalui beberapa metode. Sebagian besar metode bergantung pada informasi penomoran kursi penumpang pada masing-masing bus (atau penggunaan aksioma pemilihan terhitung). Secara umum, fungsi pemasang apapun dapat digunakan untuk menyelesaikan permasalahan ini. Untuk setiap metode-metode berikut, misalkan $k$ menyatakan nomor kursi dari penumpang yang bersangkutan, dan $b$ menyatakan nomor bus yang mengangkut penumpang tersebut. Nantinya $k$ dan $b$ akan menjadi argumen dari fungsi pemasangnya.

Metode prima berpangkat

Setiap tamu yang menghuni kamar nomor $n$ dipindahkan ke kamar nomor $2^{n}$ , lalu tempatkan penumpang ke- $k$ dari bus pertama ke kamar nomor $3^{k}$ , kemudian penumpang ke- $k$ dari bus kedua ditempatkan pada kamar nomor $5^{k}$ , dan secara umum, penumpang ke- $k$ dari bus ke- $b$ akan menghuni kamar nomor $\left(p_{b+1}\right)^{k}$ , dengan $p_{b}$ menyatakan bilangan prima ke- $b$ .

Metode ini membuat beberapa kamar tidak terisi (yang mungkin saja berguna bagi pihak hotel), yaitu kamar-kamar yang bukan merupakan bilangan prima berpangkat, seperti kamar nomor $15$ dan $847$ .

Metode faktorisasi prima

Setiap tamu yang menghuni kamar nomor $n$ dipindahkan ke kamar nomor $2^{n}$ , lalu penumpang ke- $k$ dari bus ke- $b$ akan menghuni kamar nomor $2^{k}\cdot 3^{b}$ . Oleh karena setiap bilangan memiliki hasil faktorisasi prima yang tunggal, maka jelas bahwa setiap orang akan mendapatkan kamar, dan dua orang berbeda akan menghuni kamar yang berbeda. Sebagai contoh, penghuni kamar nomor $2592$ ( $2^{5}\cdot 3^{4}$ ) berasal dari kursi ke-5 pada bus ke-4. Serupa seperti metode prima berpangkat, metode ini tidak mengisi seluruh kamar yang ada.

Metode ini dapat dengan mudah diperluas untuk jumlah malam yang tak terhingga, akses masuk yang tak terhingga, dll. ( $2^{k}\cdot 3^{b}\cdot 5^{m}\cdot 7^{a}\cdot \ldots$ )

Metode penjalinan

Setiap tamu yang menghuni kamar nomor $n$ dipindahkan ke kamar nomor $n'$ , yang diperoleh dengan menyelipkan bilangan $0$ diantara semua digit dari $n$ . Sebagai contoh, tamu penghuni kamar nomor $1729$ dipindahkan ke kamar nomor $1070209$ . Untuk setiap penumpang, bandingkan banyaknya digit dari nomor kursi $k$ dan nomor bus $b$ . Jika banyaknya digit dari $k$ berbeda dengan banyaknya digit dari $b$ , maka tambahkan awalan nol sampai keduanya memiliki banyak digit yang sama, kemudian digit-digitnya dapat dijalin untuk menghasilkan nomor kamar sebagai berikut: $\left({\text{digit ke-1 dari }}b\right)\left({\text{digit ke-1 dari }}k\right)\left({\text{digit ke-2 dari }}b\right)\left({\text{digit ke-2 dari }}k\right)\ldots$ Sebagai contoh, misalkan seorang penumpang berasal dari bus ke- ${\color {blue}789}$ dengan nomor kursi ${\color {red}12345}$ . Oleh karena banyaknya digit pada nomor bus (3 digit) berbeda dengan banyaknya digit pada nomor kursi (5 digit), tulis ${\color {blue}789}$ sebagai ${\color {blue}00789}$ (sehingga nomor bus dan nomor kursi sama-sama memiliki 5 digit). Dengan aturan penjalinan di atas, maka penumpang tersebut akan ditempatkan pada kamar nomor ${\color {blue}0}{\color {red}1}{\color {blue}0}{\color {red}2}{\color {blue}7}{\color {red}3}{\color {blue}8}{\color {red}4}{\color {blue}5}{\color {red}9}$ .

Dibandingkan dengan metode prima berpangkat, metode ini mengisi seluruh kamar hotel, dan setiap penghuni kamar dapat dikembalikan ke bus dan kursinya masing-masing dengan membalik proses penjalinannya, kemudian uraikan bilangannya menjadi dua bilangan; digit-digit pada posisi ganjil merupakan nomor bus $b$ , sedangkan digit-digit pada posisi genap merupakan nomor kursi $k$ . Cara penomorannya dapat dibalik menjadi $\left({\text{digit ke-1 dari }}k\right)\left({\text{digit ke-1 dari }}b\right)\left({\text{digit ke-2 dari }}k\right)\left({\text{digit ke-2 dari }}b\right)\ldots$ namun aturan penomorannya harus konsisten diterapkan ke seluruh penumpang.

Metode bilangan segitiga

Setiap tamu yang menghuni kamar nomor $n$ dipindahkan ke kamar nomor $T_{n}$ , yaitu bilangan segitiga ke- $n$ yang diperoleh melalui rumus $T_{n}={\dfrac {n\left(n+1\right)}{2}}$ Setiap penumpang bus ke- $b$ dengan nomor kursi $k$ akan ditempatkan pada kamar nomor $T_{b+k-1}+n$ . Dengan cara ini, maka seluruh kamar akan terisi oleh satu dan hanya satu orang.

Fungsi pemasang ini dapat divisualkan sebagai piramida dengan tinggi yang tak terhingga sebagai berikut: ${\begin{matrix}&&&&&{\color {red}1}\\&&&&2&{\color {red}3}\\&&&4&5&{\color {red}6}\\&&7&8&9&{\color {red}10}\\&11&12&13&14&{\color {red}15}\\16&\vdots &\vdots &\vdots &\vdots &{\color {red}\vdots }\end{matrix}}$ Puncak (atau baris pertama) piramidanya terdiri dari satu kamar, yaitu kamar nomor $1$ , baris kedua piramidanya terdiri dari kamar nomor $2$ dan $3$ , dan seterusnya. Kolom paling kiri menyatakan kamar-kamar yang bernomor bilangan segitiga. Setelah semua tamu hotel dipindahkan ke kamar-kamar yang berada pada kolom paling kiri, semua kamar kosong yang tersisa membentuk bangun piramida yang identik dengan bentuk awalnya. Dengan menggunakan rumus sebelumnya, setiap pendatang baru dapat menentukan ruang mana yang akan ditempati nantinya.

Metode enumerasi sembarang

Misalkan $H:=\mathbb {W} \times \mathbb {W} =\left\{\left(a,\,b\right)\mid a,b\in \mathbb {N} \cup \left\{0\right\}\right\}$ . Oleh karena $\mathbb {N}$ merupakan himpunan terhitung, maka $H$ juga merupakan himpunan terhitung, sehingga setiap elemennya dapat dicacah satu per satu sebagai $h_{1}$ , $h_{2}$ , dan seterusnya. Jika $h_{n}=\left(b,\,k\right)$ , maka tempatkan penumpang ke- $k$ dari bus ke- $b$ ke kamar nomor $n$ (anggap tamu yang sudah berada pada hotel sebagai penumpang dari bus ke- $0$ ). Dengan cara ini, maka berhasil dikonstruksikan suatu fungsi yang mengawankan setiap orang dengan suatu kamar. Lebih lanjut, proses pengawanan ini tidak melewati satu ruang pun.

Lapisan takhingga yang lebih banyak

Misalkan lokasi hotelnya berada di sebelah lautan, dan datang takhingga banyaknya kapal feri, yang masing-masing mengangkut takhingga banyaknya bus, yang masing-masing mengangkut takhingga banyaknya penumpang. Situasi seperti ini melibatkan tiga "lapisan" takhingga, dan dapat diselesaikan dengan perluasan dari metode-metode yang telah dipaparkan sebelumnya.

Metode faktorisasi prima dapat diterapkan dengan menambakan bilangan prima baru untuk setiap lapisan takhingga tambahan. Dalam konteks tiga lapisan, maka setiap penumpang ke- $k$ dari bus ke- $b$ pada kapal feri ke- $f$ akan ditempatkan pada kamar nomor $2^{k}\cdot 3^{b}\cdot 5^{f}$ .

Metode prima berpangkat dapat diterapkan dengan proses pemangkatan bilangan prima lebih lanjut, yang menghasilkan bilangan yang besar sekalipun nilai masukannya cukup kecil. Dalam konteks tiga lapisan, maka setiap penumpang ke- $k$ dari bus ke- $b$ pada kapal feri ke- $f$ akan ditempatkan pada kamar nomor $\left(p_{f+1}\right)^{\left(p_{b+1}\right)^{k}}$ , dengan $p_{i}$ menyatakan bilangan prima ke- $i$ . Sebagai contoh, penumpang ke- $2$ dari bus ke- $3$ pada kapal feri ke- $2$ akan menghuni kamar nomor $5^{7^{2}}$ , yang memiliki lebih dari 30 digit desimal.

Metode penjalinan dapat digunakan dengan menjalin beberapa "untaian" secara bergantian. Dalam konteks tiga lapisan, penumpang maka setiap penumpang ke- $k$ dari bus ke- $b$ pada kapal feri ke- $f$ akan ditempatkan pada kamar nomor sebagai berikut: $\left({\text{digit ke-1 dari }}k\right)\left({\text{digit ke-1 dari }}b\right)\left({\text{digit ke-1 dari }}f\right)\left({\text{digit ke-2 dari }}k\right)\left({\text{digit ke-2 dari }}b\right)\left({\text{digit ke-2 dari }}f\right)\ldots$ Jika banyaknya digit dari $k$ , $b$ , dan $f$ tidaklah sama, maka tambahkan awalan nol sampai ketiganya memiliki banyak digit yang sama. Sebagai contoh, penumpang ke- ${\color {red}2}$ dari bus ke- ${\color {blue}5}$ pada kapal feri ke- ${\color {green}4}$ akan menghuni kamar nomor ${\color {red}2}{\color {blue}5}{\color {green}4}$ , dan penumpang ke- ${\color {red}4935}$ dari bus ke- ${\color {blue}198}$ pada kapal feri ke- ${\color {green}82217}$ akan menghuni kamar nomor ${\color {red}0}{\color {blue}0}{\color {green}8}{\color {red}4}{\color {blue}0}{\color {green}2}{\color {red}9}{\color {blue}1}{\color {green}2}{\color {red}3}{\color {blue}9}{\color {green}1}{\color {red}5}{\color {blue}8}{\color {green}7}$ .

Analisis

Paradoks Hotel Hilbert merupakan paradoks veridikal: hasilnya bersifat kontraintuitif namun dapat dibuktikan kebenarannya. Pernyataan "setiap kamar memiliki penghuni" dan "tidak dapat mengakomodasi tamu tambahan" tidak lagi ekuivalen ketika terdapat tak terhingga banyaknya kamar.

Pada awalnya, kondisi ini terlihat kontraintuitif. Sifat-sifat dari himpunan-himpunan takhingga cukup berbeda dengan sifat-sifat dari himpunan berhingga. Paradoks hotel Hilbert dapat dipahami melalui teori bilangan transfinit Cantor. Dalam hotel biasa (dengan jumlah kamar yang terbatas), banyaknya kamar bernomor ganjil jelas kurang dari banyaknya kamar pada hotel tersebut. Akan tetapi, dalam hotel Hilbert, banyaknya kamar bernomor ganjil tidak kurang dari "banyaknya" kamar yang ada.

Dengan istilah matematika, kardinalitas dari suatu himpunan bagian yang memuat kamar bernomor ganjil sama dengan kardinalitas dari himpunan semua kamar. Himpunan takhingga dikarakterkan sebagai himpunan yang memiliki himpunan bagian sejati yang kardinalitasnya sama. Untuk himpunan terhitung (yaitu himpunan yang memiliki kardinalitas yang sama dengan bilangan asli), kardinalitasnya ialah $\aleph _{0}$ .^[3]

Dengan kata lain, untuk setiap himpunan terhitung takhingga, terdapat suatu fungsi bijektif yang memetakan himpunan terhitung takhingga ke bilangan asli, meskipun himpunan terhitung takhingganya memuat bilangan-bilangan asli. Sebagai contoh, himpunan bilangan rasional — bilangan-bilangan yang dapat dinyatakan sebagai perbandingan dari bilangan bulat — memuat bilangan asli sebagai himpunan bagiannya, namun himpunan tersebut tidaknya lebih besar dari himpunan bilangan asli, sebab bilangan rasional merupakan himpunan terhitung: terdapat bijeksi dari bilangan asli ke bilangan rasional.

Lihat juga

Referensi

^ Kragh, Helge (2014). "The True (?) Story of Hilbert's Infinite Hotel". arΧiv:1403.0059 [physics.hist-ph].
^ Gamow, George (1947). One Two Three... Infinity: Facts and Speculations of Science (dalam bahasa Inggris). New York: Viking Press. hlm. 17.
^ Rucker, Rudy (1984) [1982]. Infinity and the Mind. The Science and Philosophy of the Infinite (dalam bahasa Inggris). Paladin. hlm. 73–78. ISBN 0-586-08465-7.

Hilbert, David (2013), Ewald, William; Sieg, Wilfried, ed., David Hilbert's Lectures on the Foundations of Arithmetics and Logic 1917-1933, Heidelberg: Springer-Verlag, doi:10.1007/978-3-540-69444-1, ISBN 978-3-540-20578-4

[1] Kragh, Helge (2014). "The True (?) Story of Hilbert's Infinite Hotel". arΧiv:1403.0059 [physics.hist-ph].

[2] Gamow, George (1947). One Two Three... Infinity: Facts and Speculations of Science (dalam bahasa Inggris). New York: Viking Press. hlm. 17.

[Rucker-3] Rucker, Rudy (1984) [1982]. Infinity and the Mind. The Science and Philosophy of the Infinite (dalam bahasa Inggris). Paladin. hlm. 73–78. ISBN 0-586-08465-7.

[1]

[2]

[3]