Kurva bidang kuartik
Artikel atau sebagian dari artikel ini mungkin diterjemahkan dari Quartic plane curve di en.wikipedia.org. Isinya masih belum akurat, karena bagian yang diterjemahkan masih perlu diperhalus dan disempurnakan. Jika Anda menguasai bahasa aslinya, harap pertimbangkan untuk menelusuri referensinya dan menyempurnakan terjemahan ini. Anda juga dapat ikut bergotong royong pada ProyekWiki Perbaikan Terjemahan. (Pesan ini dapat dihapus jika terjemahan dirasa sudah cukup tepat. Lihat pula: panduan penerjemahan artikel) |
Kurva bidang kuartik merupakan sebuah kurva aljabar bidang dari derajat empat. Ini dapat didefinisikan oleh sebuah persamaan kuartik bivariasi:
dengan setidaknya salah satu dari , , , , taksama dengan nol. Persamaan ini memiliki 15 konstanta. Namun, ini dapat dikalikan dengan setiap konstanta taknol tanpa mengubah kurva, demikian dengan pilihan konstanta yang tepat dari perkalian, setiap salah satu dair keofisien dapat dihimpunkan menjadi 1, meninggalkan hanya 14 konstanta. Oleh karena itu, ruang kurva kuartik dapat diidentifikasi dengan ruang projektif real . Ini juga diikuti, dari teorema Cramer pada kurva aljabar, yang terdapat satu kurva kuartik yang lewat melalui sebuah himpunan dari 14 titik yang berbeda dalam posisi umum, karena sebuah kuartik memiliki 14 derajat kebebasan
Sebuah kurva kuartik dapat memiliki sebuah maksimum dari:
- Empat komponen yang terhubung
- Duapuluhdelapan bitangen
- Tiga titik ganda biasa
Salah satunya dapat dianggap kurva kuadrik pada medan lain (atau bahkan gelanggang). Dalam cara ini, salah satunya mendapatkan permukaan Riemann, yang merupakan objek satu dimensi pada , tetapi merupakan dua dimensi pada . Sebuah contohnya adalah kuartik Klein. Sebagai tambahan, salah satunya dapat dilihat di kurva dalam bidang proyektif, diberikan oleh polinomial homogen.
Contoh-contoh
[sunting | sunting sumber]Berbagai kombinasi koefisien dalam persamaan di atas menimbulkan berbagai keluarga-keluarga kurva yang penting seperti yang didaftarkan di bawah.
-
Kurva Ampersand
-
Kurva kacang
-
Kurva bikuspid
-
Kurva ikatan simpul
-
Kurva silang dengan parameter menjadi di warna merah; di warna hijau; serta di warna biru.
-
Kurva silang dengan parameter menjadi di warna merah; di warna hijau; serta di warna biru.
-
Semanggi berdaun tiga dalam koordinat Kartesius.
-
Semanggi berdaun tiga dalam koordinat polar.
Kurva Ampersand
[sunting | sunting sumber]Kurva Ampersand merupakan sebuah kurva bidang kuartik diberikan oleh persamaan:
Ini memiliki genus nol, dengan tiga titik ganda biasa, semuanya di bidang real.[1]
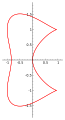
Kurva kacang
[sunting | sunting sumber]Kurva kacang merupakan sebuah kurva bidang kuartik dengan persamaan:
Kurva kacang memiliki genus nol. Ini memiliki sebuah singularitas pada asalnya, pada titik rangkap-tiga biasa.[2][3]
Kurva bikuspid
[sunting | sunting sumber]Bikuspid merupakan sebuah kurva bidang kuartik dengan persamaan
dimana menentukan ukuran dari kurva. Bikuspid hanya memiliki dua simpul sebagai singularitas, dan karena itu merupakan sebuah kurva genus satu.[4]
Kurva ikatan simpul
[sunting | sunting sumber]Kurva ikatan simpul merupakan sebuah kurva bidang kuartik dengan persamaan
Kurva ikatan simpul memiliki sbeuah titik rangkap-tiga yang tunggal pada , , dan akibatnya merupakan sebuah kurva rasional, dengan genus nol.[5]
Kurva silang
[sunting | sunting sumber]Kurva silang merupakan sebuah kurva bidang kuartik diberikan oleh persamaan
dimana dan adalah dua parameter yang menentukan bentuk dari kurva. Kurva silang berkaitan oleh sebuah transformasi kuadratik standar, , ke elips , dan oleh karena itu merupakan sebuah kurva aljabar bidang rasional dari genus nol. Kurva silang memiliki tiga titik ganda dalam bidang proyektif real, pada dan , dan , serta dan .[6]
Karena kurvanya adalah rasional, ini dapat diparameterkan sebagai fungsi rasional. Sebagai contoh, jika dan , maka
memparameter titik-titiknya pada kurva di luar dari kasus istimewa dimana sebuah pembilang adalah nol.
Irisan spirik
[sunting | sunting sumber]Irisan spirik dapat didefinisikan sebagai kurva kuartik bisirkular yang simetri terhadap sumbu x dan y. Irisan spirik termasuk dalam keluarga irisan torik dan termasuk keluarga hippopedes dan keluarga oval Cassini. Namanya dari σπειρα berarti torus dalam Yunani kuno.
Persamaan Kartesius dapat ditulis sebagai
dan persamaan dalam koordinat polar sebagai
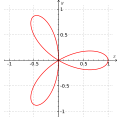
Semanggi berdaun tiga (trifolium)
[sunting | sunting sumber]Semanggi berdaun tiga atau trifolium[7] merupakan kurva bidang kuartik
Dengan menyelesaikan untuk , kurvanya dapat digambarkan oleh fungsi berikut
dimana dua kemunculan dari ± adalah bebas satu sama lain, menyerahkan empat nilai yang berbeda dari untuk setiap .
Persamaan parametrik kurva adalah[8]
Dalam koordinat polar, yaitu dan , persamaannya adalah
Ini adalah sebuah kasus khusus kurva mawar dengan . Kurva ini memiliki sebuah titik rangkap-tifa pada di asalnya dan memiliki tiga garis singgung ganda.
Lihat pula
[sunting | sunting sumber]Referensi
[sunting | sunting sumber]- ^ (Inggris) Weisstein, Eric W. "Ampersand Curve". MathWorld.
- ^ Cundy, H. Martyn; Rollett, A. P. (1961) [1952], Mathematical models (edisi ke-2nd), Clarendon Press, Oxford, hlm. 72, ISBN 978-0-906212-20-2, MR 0124167
- ^ (Inggris) Weisstein, Eric W. "Bean Curve". MathWorld.
- ^ (Inggris) Weisstein, Eric W. "Bicuspid Curve". MathWorld.
- ^ (Inggris) Weisstein, Eric W. "Bow". MathWorld.
- ^ (Inggris) Weisstein, Eric W. "Cruciform curve". MathWorld.
- ^ (Inggris) Weisstein, Eric W. "Trifolium". MathWorld.
- ^ Gibson, C. G., Elementary Geometry of Algebraic Curves, an Undergraduate Introduction, Cambridge University Press, Cambridge, 2001, ISBN 978-0-521-64641-3.